Hyperbolas are great, they're used to describe gravity assists, the shape power lines or chains make when hanging off two points is a Catenary.
This post is about the hyperbolic functions that describe hyperbolics parametrically. In particular I show how you might have discovered them yourself!
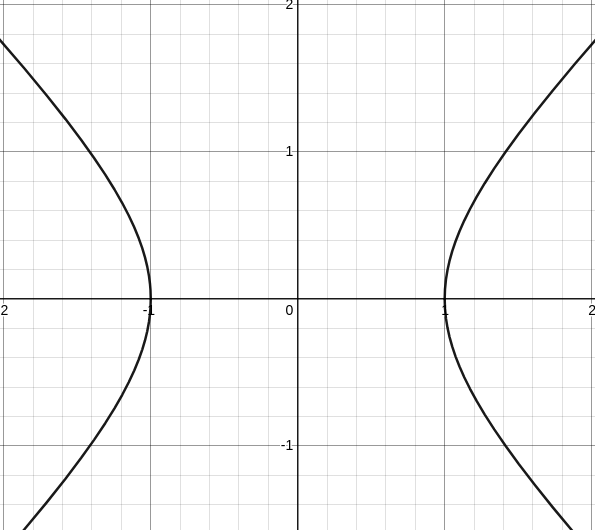
This is the unit hyperbola, described by . We want to find that describe this curve. Since they are always on the curve they must satisfy
Knowing how change will help us find and , so let's differentiate using implicit differentiation
Hey! That means and for some constant (since rational numbers are unique up to a constant multiple) This reminds me of , except there are two functions in a cycle instead of one.
We can use this to find all the derivatives in terms of and
Hey! If differentiating gives us and vise versa, then differentiating should stay the same up to a multiple of , Let's do this
If we denote to be the sum then we have .
This reminds me of since it's derivative is times itself, so I'm going to write as a Maclaurin Series and try to find in terms of , but first we need to decide what is, let's look at the graph again

Where should our parametric equations start? All points work fine, but we'll pick for two reasons
- It's a natural seeming starting point
- Having will drastically simplify our maclaurin series
Now that we have our starting point, we can find the maclaurin series of
You might recognize this series, it's the series for !, therefor
Now I want to find and individually, going back to the original equation I notice it's a difference of squares, meaning we can factor it as
Adding the sum and difference we can recover the individual equations!
Let's check our work, our functions should satisfy
Great! our and work, and they are and when .
Arc length reparameterization
Picking seems like an arbitrary choice, let's try to reparameterize in terms of arc length to give geometric meaning
You can try to evaluate this integral, but you can't! this is a Nonelementary integral (see wolframalpha).
Relation to other conics
If you noticed the similarity between (for describing hyperbolas) and (for describing circles and ellipses) You might be wondering about expressing other conics parametrically.
The only other conic is a parabola (as circles are a special case of an ellipse). parabolas are described by , which is already a function!
Visually parabolas (3) look different from the other conics, they just barely hug the cone
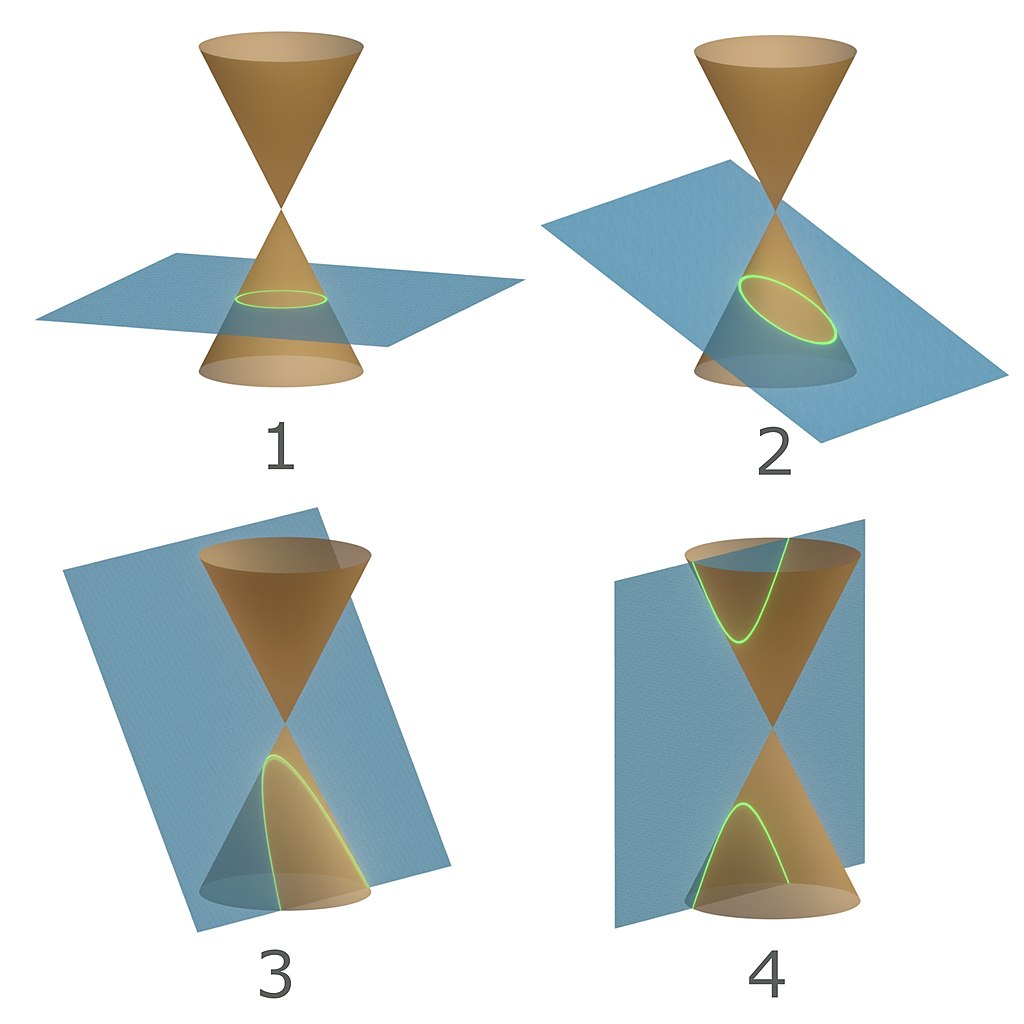
I like to think of this in terms of their Eccentricity
- Ellipses have eccentricity less then one
- Parabolas have eccentricity equal to one
- Hyperbolas have eccentriciy greater then one
Parabolas really are the special child in the family! They are the only conic with a single eccentricity. Here's a desmos graph showing this off
I plan to write about parabolas some time, since they show up everywhere in algebra I want to become more acquainted with their amazing properties
