Cauchy Theorem
In general we have
n ! 2 π i ∮ f ( z ) ( z − p ) n + 1 d z = f ( n ) ( p ) \frac{n!}{2\pi i} \oint \frac{f(z)}{(z-p)^{n+1}}dz = f^{(n)}(p) 2 πi n ! ∮ ( z − p ) n + 1 f ( z ) d z = f ( n ) ( p ) Which can be proven from the power series of f ( z ) f(z) f ( z ) ∮ 1 / z = 2 π i \oint 1/z = 2\pi i ∮ 1/ z = 2 πi ∮ 1 / z n = 0 \oint 1/z^n = 0 ∮ 1/ z n = 0
The interesting bit is that defining the taylor coefficients like this also works, meaning a smooth complex function has a power series! You prove this with cursed analysis.
Residue theorem
A residue takes a pole α \alpha α
f ( z ) = h ( z ) ( z − α ) n f(z) = \frac{h(z)}{(z-\alpha)^n} f ( z ) = ( z − α ) n h ( z ) Where h ( z ) h(z) h ( z ) z = α z = \alpha z = α
h ( n − 1 ) ( α ) ( n − 1 ) ! \frac{h^{(n-1)}(\alpha)}{(n-1)!} ( n − 1 )! h ( n − 1 ) ( α ) The residue theorem is that
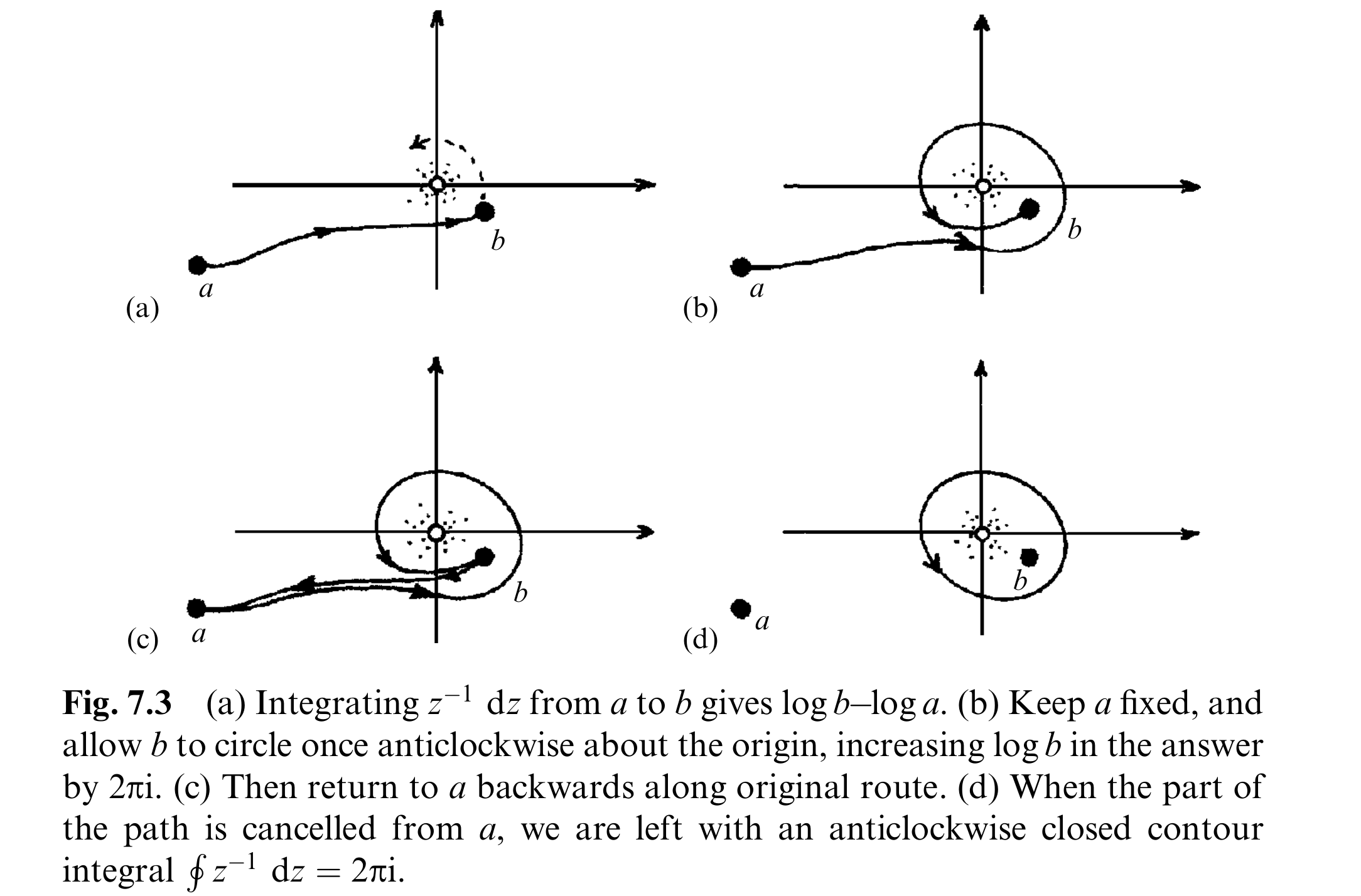
∮ r f ( z ) d z = 2 π i × { sum of residues } \oint_r f(z)dz = 2\pi i \;\times \; \left\{\text{sum of residues}\right\} ∮ r f ( z ) d z = 2 πi × { sum of residues } Prove this by contracting around each pole to get
f ( z ) = h ( n − 1 ) ( α ) ( z − α ) n f(z) = \frac{h^{(n-1)}(\alpha)}{(z-\alpha)^n} f ( z ) = ( z − α ) n h ( n − 1 ) ( α ) α \alpha α
∮ r f ( z ) d z = ∮ { ∑ i = 1 n h i ( z ) ( z − α i ) n i } d z = 2 π i { ∑ i = 1 n h i ( n i − 1 ) ( α i ) ( n i − 1 ) ! } \oint_r f(z)dz
= \oint \left\{\sum_{i=1}^{n} \frac{h_i(z)}{(z-\alpha_i)^{n_i}}\right\}dz
= 2\pi i \left\{\sum_{i=1}^n \frac{h_i^{(n_i-1)}(\alpha_i)}{(n_i-1)!}\right\} ∮ r f ( z ) d z = ∮ { i = 1 ∑ n ( z − α i ) n i h i ( z ) } d z = 2 πi { i = 1 ∑ n ( n i − 1 )! h i ( n i − 1 ) ( α i ) } 7.6
We're going to show ∑ 1 / n 2 = π 2 / 6 \sum 1/n^2 = \pi^2/6 ∑ 1/ n 2 = π 2 /6 2 N + 1 2N+1 2 N + 1 N → ∞ N \to \infty N → ∞
First use the residue theorem on
∮ z − 2 cot ( π z ) d z \oint z^{-2}\cot{(\pi z)}dz ∮ z − 2 cot ( π z ) d z There's a pole at every z ∈ Z z \in \mathbf{Z} z ∈ Z z = 0 z = 0 z = 0 z ∈ Z ∖ { 0 } z \in \mathbf{Z}\setminus \{0\} z ∈ Z ∖ { 0 }
Let α ∈ Z ∖ { 0 } \alpha \in \mathbf{Z} \setminus \{0\} α ∈ Z ∖ { 0 }
f ( z ) = z − 2 cot ( π z ) = h ( z ) ( z − α ) f(z) = z^{-2}\cot(\pi z) = \frac{h(z)}{(z - \alpha)} f ( z ) = z − 2 cot ( π z ) = ( z − α ) h ( z ) For regular h ( z ) h(z) h ( z ) h ( z ) = z − α z 2 cot ( π z ) h(z) = \frac{z-\alpha}{z^2}\cot(\pi z) h ( z ) = z 2 z − α cot ( π z ) h ( 0 ) ( α ) / 0 ! = lim z → α h ( z ) h^{(0)}(\alpha)/0! = \lim_{z \to \alpha} h(z) h ( 0 ) ( α ) /0 ! = lim z → α h ( z )
lim z → α z − α z 2 cos ( π z ) sin ( π z ) = lim z → α 1 π z 2 = 1 π α 2 \lim_{z \to \alpha} \frac{z-\alpha}{z^2} \frac{\cos(\pi z)}{\sin(\pi z)} = \lim_{z \to \alpha} \frac{1}{\pi z^2} = \frac{1}{\pi \alpha^2} z → α lim z 2 z − α sin ( π z ) cos ( π z ) = z → α lim π z 2 1 = π α 2 1 (This is where we get the 1 / n 2 1/n^2 1/ n 2
Now consider the pole at z = 0 z = 0 z = 0 3 3 3 2 2 2 z − 2 z^{-2} z − 2 1 1 1 cot ( π z ) \cot(\pi z) cot ( π z )
h ( z ) = z 3 cot ( π z ) z 2 = z cot ( π z ) h(z) = \frac{z^3 \cot(\pi z)}{z^2} = z\cot(\pi z) h ( z ) = z 2 z 3 cot ( π z ) = z cot ( π z ) Computing the residue means computing h ( 2 ) ( 0 ) / 2 ! h^{(2)}(0)/2! h ( 2 ) ( 0 ) /2 !
h ( 2 ) ( z ) 2 ! = π ( π z cot ( π z ) − 1 ) csc 2 ( π z ) \frac{h^{(2)}(z)}{2!} = \pi(\pi z\cot(\pi z) - 1)\csc^2(\pi z) 2 ! h ( 2 ) ( z ) = π ( π z cot ( π z ) − 1 ) csc 2 ( π z ) As z → 0 z \to 0 z → 0 − π / 3 -\pi/3 − π /3
∮ z − 2 cot ( π z ) d z = 2 π i ( − π 3 + 2 ∑ i = 1 N 1 π n 2 ) \oint z^{-2}\cot{(\pi z)}dz = 2\pi i\left(-\frac{\pi}{3} + 2\sum_{i=1}^{N}
\frac{1}{\pi n^2} \right) ∮ z − 2 cot ( π z ) d z = 2 πi ( − 3 π + 2 i = 1 ∑ N π n 2 1 ) If we can just show this integral goes to zero as N → ∞ N \to \infty N → ∞
∑ i = 1 N 1 n 2 → π 2 6 \sum_{i=1}^N \frac{1}{n^2} \to \frac{\pi^2}{6} i = 1 ∑ N n 2 1 → 6 π 2 We show the integral goes to zero by bounding the integrand via a constant, since all constants have zero contour integral. It's possible to show
∣ cot ( π z ) ∣ ≤ 2 (for large N and z on the 2 N + 1 box boundary) |\cot(\pi z)| \le 2 \quad\text{(for large $N$ and $z$ on the $2N+1$ box boundary)} ∣ cot ( π z ) ∣ ≤ 2 (for large N and z on the 2 N + 1 box boundary) Using Eulers formula and some algebra. First use the formula
cot ( π z ) = e i π z + e − i π z e i π z − e − i π z = 1 + e − 2 π i z 1 − e − 2 π i z \cot(\pi z) = \frac{e^{i \pi z} + e^{-i\pi z}}{e^{i\pi z} - e^{-i\pi z}} = \frac{1 + e^{-2\pi i z}}{1 - e^{-2\pi i z}} cot ( π z ) = e iπ z − e − iπ z e iπ z + e − iπ z = 1 − e − 2 πi z 1 + e − 2 πi z Then set z = ( N + 1 / 2 ) + i w z = (N+1/2) + iw z = ( N + 1/2 ) + i w
cot ( π ( 2 N + 1 ) + i w ) = 1 + e − 2 π i ( N + 1 / 2 ) e − 2 π i ( i w ) 1 − e − 2 π i ( N + 1 / 2 ) e − 2 π i ( i w ) = 1 − e − 2 π i ( i w ) 1 + e − 2 π i ( i w ) = 1 − e 2 π w 1 + e 2 π w \begin{aligned}
\cot(\pi (2N+1) + iw)
&= \frac{1 + e^{-2\pi i(N+1/2)}e^{-2\pi i(iw)}}{1 - e^{-2\pi i(N+1/2)}e^{-2\pi i(iw)}} \\
&= \frac{1 - e^{-2\pi i(iw)}}{1 + e^{-2\pi i(iw)}} \\
&= \frac{1 - e^{2\pi w}}{1 + e^{2\pi w}}
\end{aligned} cot ( π ( 2 N + 1 ) + i w ) = 1 − e − 2 πi ( N + 1/2 ) e − 2 πi ( i w ) 1 + e − 2 πi ( N + 1/2 ) e − 2 πi ( i w ) = 1 + e − 2 πi ( i w ) 1 − e − 2 πi ( i w ) = 1 + e 2 π w 1 − e 2 π w At this point you either realize this equals tanh ( 2 π w ) \tanh(2\pi w) tanh ( 2 π w ) 1 1 1
∣ 1 − e x 1 + e x ∣ = ∣ 2 1 + e x − 1 ∣ < 1 \left|\frac{1 - e^{x}}{1 + e^x}\right| = \left|\frac{2}{1 + e^x} - 1\right| < 1 ∣ ∣ 1 + e x 1 − e x ∣ ∣ = ∣ ∣ 1 + e x 2 − 1 ∣ ∣ < 1 Now for the horizontal ones set z = w + i ( N + 1 / 2 ) z = w + i(N+1/2) z = w + i ( N + 1/2 )
cot ( π z ) = 1 + e − 2 π i w e 2 π ( N + 1 / 2 ) 1 − e − 2 π i w e 2 π ( N + 1 / 2 ) \begin{aligned}
\cot(\pi z)
&= \frac{1 + e^{-2\pi iw}e^{2\pi (N+1/2)}}{1 - e^{-2\pi iw} e^{2\pi (N+1/2)}}
\end{aligned} cot ( π z ) = 1 − e − 2 πi w e 2 π ( N + 1/2 ) 1 + e − 2 πi w e 2 π ( N + 1/2 ) The e − 2 π i w e^{-2\pi i w} e − 2 πi w 1 1 1 N → ∞ N \to \infty N → ∞ e 2 π ( N + 1 / 2 ) e^{2\pi (N+1/2)} e 2 π ( N + 1/2 ) 1 1 1 ϵ > 0 \epsilon > 0 ϵ > 0 N N N
∣ 1 + e − 2 π i w e 2 π ( N + 1 / 2 ) 1 − e − 2 π i w e 2 π ( N + 1 / 2 ) ∣ ≤ 1 + ϵ \left|
\frac{1 + e^{-2\pi iw}e^{2\pi (N+1/2)}}{1 - e^{-2\pi iw} e^{2\pi (N+1/2)}}\right| \le 1 + \epsilon ∣ ∣ 1 − e − 2 πi w e 2 π ( N + 1/2 ) 1 + e − 2 πi w e 2 π ( N + 1/2 ) ∣ ∣ ≤ 1 + ϵ Setting ϵ = 1 \epsilon = 1 ϵ = 1
∣ cot ( π z ) z 2 ∣ ≤ 2 N 2 \left|\frac{\cot(\pi z)}{z^2}\right| \le \frac{2}{N^2} ∣ ∣ z 2 cot ( π z ) ∣ ∣ ≤ N 2 2 Which multiplied by the perimeter 4 ( 2 N + 1 ) 4(2N+1) 4 ( 2 N + 1 )
∣ ∮ z − 2 cot ( π z ) d z ∣ ≤ ∣ ∫ P 2 N 2 d z ∣ ≤ ( 2 N 2 ) ( 8 N + 4 ) ≤ 20 N \left|\oint z^{-2}\cot(\pi z)dz\right| \le \left|\int_P \frac{2}{N^2}dz\right| \le \left(\frac{2}{N^2}\right)\left(8N+4\right) \le \frac{20}{N} ∣ ∣ ∮ z − 2 cot ( π z ) d z ∣ ∣ ≤ ∣ ∣ ∫ P N 2 2 d z ∣ ∣ ≤ ( N 2 2 ) ( 8 N + 4 ) ≤ N 20 This goes to zero as N → ∞ N \to \infty N → ∞

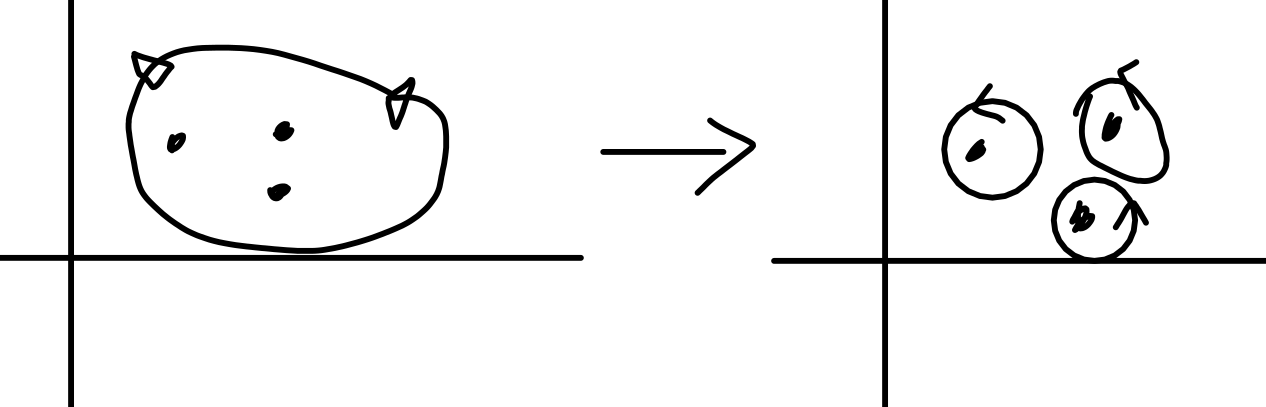 Which, after writing around each pole and summing gives
Which, after writing around each pole and summing gives