See also: Six and a half intuitions for kl divergence.

The cross entropy is defined as the expected surprise when drawing from $p(x)$, which we're modeling as $q(x)$. Our map is $q(x)$ while $p(x)$ is the territory.

Now it should be intuitively clear that $H(p, q) \ge H(p, p)$ because an imperfect model $q(x)$ will (on average) surprise us more than the perfect model $p(x)$.

To measure unnecessary surprise from approximating $p(x)$ by $q(x)$ we define

This is KL-divergence! The average additional surprise from our map approximating the territory.

Now it's time for an exercise, in the following figure $q^{*}(x)$ is the Gaussian that minimizes $D_{\mathrm{KL}}(p\|q)$ or $D_{\mathrm{KL}}(q\|p)$, can you tell which is which?

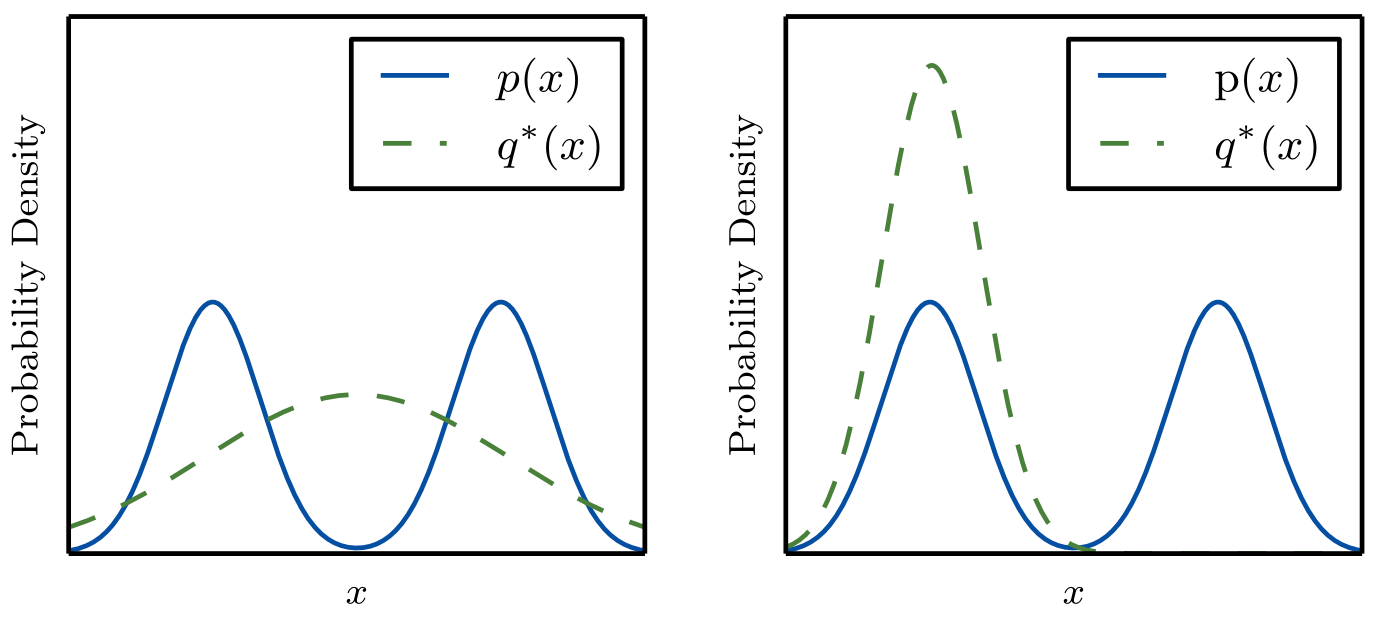
Answer

Left is minimizing $D_{\mathrm{KL}}(p\|q)$ while the right is minimizing $D_{\mathrm{KL}}(q\|p)$.

Reason as follows:

• If $p$ is the territory then the left $q^{*}$ is a better map (of $p$) than the right $q^{*}$.
• If $p$ is the map, then the territory $q^{*}$ on the right leads to us being less surprised than the territory on the left, because on the on left $p$ will be very surprised at data in the middle, despite it being likely according to the territory $q^{*}$.

On the left we fit the map to the territory, on the right we fit the territory to the map.