Optimal Polynomial Approximation

Added 2022-03-13, Modified 2022-07-20

An introduction to linear algebra and least squares on functions

Prerequisites

Know what an integral represents
Know about taylor series for approximating functions
Sufficient mathematical maturity

Introduction

If you're confused see Notation, if that doesn't clear it up contact me so I can fix the post to be more understandable.

Demo

This polynomial

0.005643 x^{5} - 0.15527 x^{3} + 0.98786 x

Is the best fifth degree polynomial approximation for $\sin x$ over $[-\pi,\pi]$ (within roundoff of course).

Do you see the two graphs? They're so close it's hard to tell there are two! If you compute the squared error (where $p(x)$ denotes our polynomial approximation)

\int_{-\pi}^\pi (\sin(x) - p(x))^2 dx = 0.000116

We find it's a really good approximation for $\sin(x)$ , taylor polynomials don't even compare with an error of $0.1187$ .

The best part? These optimal polynomial approximations can be efficiently found for any function, in fact, for complicated functions they're easier to find then taylor series!

Here's the code if you want to play with it before learning the math

Done? Okay, then get ready for...

Linear Algebra

Though a bit of an exaggeration, it can be said that a mathematical problem can be solved only if it can be reduced to a calculation in linear algebra. Thomas Garrity

Before you truely understand the demo we've got to learn some linear algebra! To be specific you need to know

Vectors and vector spaces
Subspaces
Bases
Inner products and orthogonality
Orthonormal bases
Orthogonalization

I won't be covering linear transformations (the heart of linear algebra) at all, because they aren't needed here.

Important: Attempt the exercises and read the solutions. I've put a lot of content in the solutions so skipping them will make reading this impossible.

The standard space $\mathbf R^n$

Before we get to polynomials, let's consider "vanilla" linear algebra, where every vector a list of numbers in $\mathbf R^n$ .

Adding and scaling vectors works as you'd expect

\begin{aligned} (x_1,x_2) + (y_1,y_2) &= (x_1+y_1,x_2+y_2) \\ \lambda (x_1,x_2) &= (\lambda x_1, \lambda x_2) \end{aligned}

In abstract linear algebra vectors are any object you can add and scale like this.

Exercise: Functions and Polynomials are also vectors, convince yourself of this

Solution

We can add functions and multiply by scalars and the result will still be a function, same with polynomials

The set vectors are contained in is called a vector space. A vector space has a few requirements

Closed under addition: If $v \in V$ and $w \in V$ then $w + v \in V$
Closed under scaling: If $v \in V$ and $\lambda \in \mathbf R$ then $\lambda v \in V$

Without these properties working in a vector space would be impossible, imagine adding two vectors and not knowing if the result is also in the space!

Exercise: Why must the zero vector be in every vector space?

Solution

Set $\lambda = 0$ and use (2).

Exercise: Show the space of polynomials of degree exactly $n$ is not a vector space

Solution

It doesn't contain the zero polynomial.

Exercise: Fix the problem shown in the previous exercise to get us a vector space of polynomials

Solution

Consider the space of polynomials with degree at most $n$ (denoted $\mathcal P_n$ ). This satisfies the vector space rules since

Adding polynomials of degree at most $n$ results in polynomials with degree at most $n$ , so we're closed under addition
Scaling polynomials can only decrease their degree, so we're closed under scaling

Subspaces

A vector space $U$ is said to be a subspace of $V$ if $U$ is contained in $V$ , ie. $U \subseteq V$ .

Exercise: Show the space of polynomials $\mathcal P$ (of any degree) is a subspace of all real functions (denoted $\mathbf R^{\mathbf R}$ )

Solution

The set of polynomials $\mathcal P$ is a vector space, and every polynomial is also a function, in set notation $\mathcal P \subseteq \mathbf{R}^{\mathbf R}$ . Hence $\mathcal P$ is a subspace of $\mathbf R^{\mathbf R}$ .

Exercise: Interpret our original problem of finding $n$ th degree polynomial approximations as a special case of: given a $v \in V$ find the closest $u \in U$ to $v$ (often called the projection of $v$ onto $U$ )

Solution

Consider $V = \mathbf C^{[a,b]}$ (the space of functions continuous on $[a,b]$ ) and $U = \mathcal P_n$ . then $\sin \in V$ and we want the closest $n$ th degree polynomial $p \in \mathcal P_n$ to $\sin(x)$ .

The dot product

To compute the dot product between two vectors in $\mathbf R^n$ (lists of numbers) we multiply components then add up, ie.

\langle (1,2), (3,4)\rangle = 1\cdot 3 + 2\cdot 4 = 11

As a special case the dot product of a vector with itself gives the length squared $\langle v,v\rangle = \|v\|^2$

The dot product has a very satisfying geometric interpretation: If $\theta$ is the angle between $v$ and $w$ then

\langle v, w\rangle = \|v\| \|w\|\cos\theta

Geometrically this means the dot product is the length of projecting $v$ onto the line through $w$ then scaling by $|w|$ (or the other way around). See this video for why.

Exercise: Convince yourself that $\langle u+v,w\rangle = \langle u,w\rangle+\langle v,w\rangle$ and $\lambda \langle v,w\rangle = \langle \lambda v, w\rangle$ when $\langle\cdot\rangle$ denotes the dot product.

Exercise: Using the projection interpretation, what is the projection of $v$ onto the line through $u$ ?

Solution

First normalize $u$ by dividing by it's length, then take the dot product and scale in the direction of $u$ , which we normalize again to avoid unwanted scaling

\langle v, u/\|u\|\rangle \cdot (u/\|u\|)

This is usually written as (after using linearity of $\langle\cdot\rangle$ )

\frac{\langle v, u\rangle}{\langle u, u\rangle}u

Exercise: Expand $\|v-w\|^2$ in terms of dot products, then use the geometric interpretation to prove the law of cosines.

Solution

Expand using linearity just like you would with polynomials!

\begin{aligned} \|v-w\|^2 &= \langle v-w,v-w\rangle \\ &= \langle v, v\rangle - 2\langle v, w \rangle + \langle w, w\rangle \\ &= \|v\|^2 + \|w\|^2 - 2\langle v, w\rangle \end{aligned}

Using the geometric interpretation this becomes

\|v-w\|^2 = \|v\|^2 + \|w\|^2 - 2\|v\|\|w\|\cos\theta

Which is the law of cosines!

Exercise: Compute the area of the parallelogram formed between $v$ and $w$ using dot products

Solution

Consider this diagram

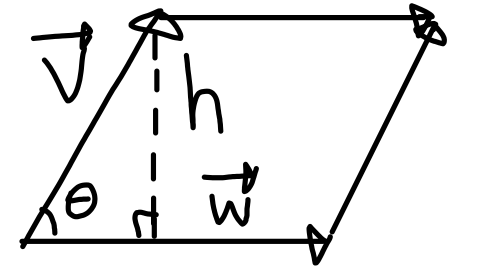
The height is $h = \|v\|\sin\theta$ meaning the area is $\|v\|\|w\|\sin\theta$ . Writing this in terms of dot products we get

\begin{aligned} \|v\|\|w\|\sin\theta &= \|v\|\|w\|\sqrt{1 - \cos^2\theta} \\ &= \|v\|\|w\|\sqrt{1 - \left(\frac{\langle v,w\rangle}{\|v\|\|w\|}\right)^2} \\ &= \sqrt{\|v\|^2\|w\|^2 - \langle v, w\rangle^2} \end{aligned}

Exercise (optional): Using the result from the previous exercise, derive the formula for the determinant of a 2x2 matrix (if you know what this means)

Solution

Suppose we have the matrix

A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}

Consider the basis vectors as $v = (a,b)$ and $w = (c,d)$ . Then the area between them is the determinant (watch these if that doesn't make sense) meaning

\begin{aligned} \det A &= \sqrt{\|v\|^2 \|w\|^2 - \langle v, w\rangle^2} \\ &= \sqrt{(a^2 + b^2)(c^2 + d^2) - (ac + bd)^2} \\ &= \sqrt{(ac)^2 + (ad)^2 + (bc)^2 + (bd)^2 - ((ac)^2 + 2acbd + (bd)^2)} \\ &= \sqrt{(ad)^2 + (bc)^2 - 2acbd} \\ &= \sqrt{(ad - bc)^2} \\ &= ad - bc \end{aligned}

General inner products

Like vectors, there can be many kinds of inner products, for instance on the space $\mathbf C^{[a,b]}$ of continuous functions on $[a,b]$ we can define an inner product

\langle f, g\rangle = \int_a^b f(x)g(x)dx

Intuitively this is the continuous version of the dot product, where we treat functions as infinite-dimensional vectors.

Like we abstracted the notion of a "vector" we also abstract the notion of an inner product to be anything that obeys a set of rules

Positivity $\langle v, v\rangle \ge 0$
Definiteness $\langle v, v\rangle = 0$ if and only if $v = 0$
Symmetry $\langle v,w\rangle = \langle w, v\rangle$
Additive $\langle u+v, w\rangle = \langle u,w\rangle + \langle v, w\rangle$
Multiplicative $\lambda\langle v,w\rangle = \langle\lambda v,w\rangle$

Exercise: Convince yourself that both inner products I've given so far satisfy these properties.

To generalize length we define the norm of a vector $v$ as $\|v\| = \sqrt{\langle v,v\rangle}$

Exercise: Generalize the law of cosines to any inner product $\langle\cdot\rangle$ .

Solution

Exactly the same steps as with the law of cosines

\begin{aligned} \|v - w\|^2 &= \langle v-w, v-w\rangle \\ &= \langle v,v\rangle - 2\langle v,w\rangle + \langle w,w\rangle \\ &= \|v\|^2 + \|w\|^2 - 2\langle v,w\rangle \end{aligned}

If we were in $\mathbf R^n$ we could use the geometric interpretation to write $\langle v,w\rangle = \|v\|\|w\|\cos\theta$ like we did for the law of cosines.

Exercise: In the geometric interpretation we showed the dot product can be used to compute the cosine of the angle between two vectors, ponder the infinite-dimensional analog of this in function space (the cosine similarity of two functions!)

Solution

With dot products we had

\cos\theta = \frac{\langle v, w\rangle}{\sqrt{\langle v,v\rangle\cdot \langle w,w\rangle}}

Since the integral inner product is just a limit of dot products as the vectors get bigger and the samples become finer, it makes sense to define the cosine similarity between functions this way. We could also extract the angle using the inverse cosine if we felt like it, and talk about the angle between functions!

Exercise (hard): Why do we need $f$ and $g$ to be continuous and not just integrable? (hint: think about property 2)

Solution

The function

f(x) = \begin{cases} 0 &{x \ne 0} \\ 1 &{x = 0} \end{cases}

Is integrable on $[-1,1]$ with $\langle f,f\rangle = \int_{-1}^1 f(x)^2dx = 0$ , but $f \ne 0$ breaking requirement 2.

Showing this can't happen with continuous functions is tricky, but it boils down to $f(x)^2 > 0$ implying there's a neighborhood around $x$ with $f(y)^2 > 0$ meaning it contributes nonzero area.

Orthogonality

We say two vectors $v$ and $w$ are orthogonal if $\langle v, w\rangle = 0$

Exercise: Prove the pythagorean theorem for an arbitrary inner product, ie. prove that $\langle v,w\rangle = 0$ implies $\|v+w\|^2 = \|v\|^2 + \|w\|^2$ .

Solution

We expand using the linearity of inner products and cancel the $2\langle v,w\rangle$ term

\begin{aligned} \|v+w\|^2 &= \langle v+w,v+w\rangle \\ &= \langle v,v\rangle + 2\langle v,w\rangle + \langle w,w\rangle \\ &= \|v\|^2 + \|w\|^2 \end{aligned}

Exercise: If $\langle \cdot\rangle$ is the dot product and $v,w \in \mathbf R^n$ are nonzero vectors, show $v$ and $w$ are orthogonal if and only if they are perpendicular (hint: use the geometric interpretation)

Solution

To see this directly notice the projection is zero exactly when $v,w$ are perpendicular. (see this video)

We can also use the geometric formula

\langle v, w\rangle = \|v\|\|w\|\cos\theta

Because $v,w$ are nonzero we have $\|v\| > 0$ and $\|w\| > 0$ meaning this is only zero when $\cos\theta = 0$ , which only happens when $\theta$ is a multiple of $90$ degrees, ie. when $v$ and $w$ are perpendicular.

Bases

A basis for a vector space $V$ is a list $v_1,\dots,v_n$ such that

Spanning: Every $v \in V$ can be written $v = a_1v_1 + \dots + a_nv_n$ for some scalars $a_1,\dots,a_n$ .
Independent: The representation of $v$ as a combination of $v_1,\dots,v_n$ is unique.

Exercise: Convince yourself $(1,0)$ and $(0,1)$ form a basis for $\mathbf R^2$

Exercise: Show $(1, 2)$ and $(0, 2)$ form a basis of $\mathbf R^2$

Solution

Every $(x,y) \in \mathbf R^2$ can be written

(x,y) = x\cdot(1,2) + \frac{y - 2x}{2}\cdot(0, 2)

Hence $(1,2), (0,2)$ is spanning, to show independence note that

a_1(1,2) + a_2(0,2) = b_1(1,2) + (0,2)b_2

Implies (via rearrangement)

(a_1-b_1)(1,2) = (b_2-a_2)(0,2)

Since the first coordinates must equal this implies $a_1-b_1 = 0$ , this implies the left hand side is zero meaning we must have $(b_2-a_2)(0, 2) = 0$ as well, implying $b_2 - a_2 = 0$ . Thus $a_1 = b_1$ and $a_2 = b_2$ and we have shown independence.

We say a basis is orthogonal if $\langle v_j, v_k\rangle = 0$ when $j \ne k$ . And we say a basis is orthonormal if it's orthogonal and $\langle v_j, v_j\rangle = 1$ (ie. the basis vectors have unit length).

Orthogonalization

Given a basis $v_1,\dots,v_n$ of $V$ it's possible to construct an orthonormal basis $e_1,\dots,e_n$ of $V$ .

Start by setting $e_1 = v_1/\|v_1\|$ so $\langle e_1,e_1\rangle = 1$ . now we want $e_2$ in terms of $v_2$ such that $\langle e_1, e_2\rangle = 0$ .

We want this to be zero, so we subtract the projection of $v_2$ onto $e_1$ (see the geometrically interpretation for why I call it a projection)

e_2 = v_2 - \langle e_1, v_2\rangle e_1

Exercise: Verify $\langle e_1, e_2\rangle = 0$ using linearity (hint: $\langle e_1,v_2\rangle$ is just a number)

Solution

\begin{aligned} \langle e_1,e_2\rangle &= \langle e_1, v_2 - \langle e_1, v_2\rangle e_1\rangle \\ &= \langle e_1, v_2\rangle - \langle e_1, v_2\rangle \langle e_1, e_1\rangle \\ &= \langle e_1, v_2\rangle - \langle e_1, v_2\rangle \\ &= 0 \end{aligned}

I left out the step where we normalize $e_2$ , but understand after we make it orthogonal we normalize it too, in programming terms $e_2 \leftarrow e_2/\|e_2\|$ .

In general we subtract the projection onto each of the previous basis vectors

e_i = v_i - \sum_{j=1}^{i-1} \langle v_i, e_j\rangle e_j

Exercise: Show $\langle e_i, e_j\rangle = 0$ (hint: without loss of generality assume $j \lt i$ )

Solution

Using the definition of $e_i$ and orthogonality gives

\begin{aligned} \langle e_j, e_i\rangle &= \left\langle e_j, v_i - \sum_{k=1}^{i-1} \langle v_i,e_k\rangle e_k\right\rangle \\ &= \langle e_j, v_i\rangle - \sum_{k=1}^{i-1} \langle v_i, e_k\rangle \langle e_j, e_k\rangle \\ &= \langle e_j, v_i\rangle - \langle v_i, e_j\rangle \langle e_j, e_j\rangle \\ &= \langle e_j, v_i\rangle - \langle v_i, e_j\rangle \\ &= 0 \end{aligned}

The key difference from the $\langle e_1,e_2\rangle$ exercise above is using the orthogonality to cancel the other terms in the sum.

Exercise: Translate the mathematical algorithm I've described into python code using numpy and test it

Solution

import numpy as np

def normalize(v):
  return v / np.sqrt(np.inner(v,v))

v = [np.array(vi) for vi in [(1,4,2), (3,2,1), (5,1,2)]]
e = [normalize(v[0])]

for i in range(1, len(v)):
  e.append(normalize(
    v[i] - sum(
      np.inner(v[i], e[j])*e[j]
      for j in range(i)
    )
  ))

# test it
for i in range(len(v)):
  for j in range(i):
    assert np.allclose(np.inner(e[i], e[j]), 0)

This method is called the Gram–Schmidt process.

Least squares

We finally get to solve the approximation problem! We have a vector space $V$ , a subspace $U$ and some vector $v \in V$ . We want to find the closest vector to $v$ in $U$ (ie. the projection).

I've you've been following along and doing the exercises you're close to understanding the method, the main ideas are:

We can write $v = a_1u_1+\dots+a_nu_n + b_1v_1+\dots+b_mv_m$ where $u_1,\dots,u_n,v_1,\dots,v_m$ is an orthonormal basis of $V$ , and $u_1,\dots,u_n$ is an orthonormal basis of $U$ .
We can extract $a_1,\dots,a_n$ using inner products and orthogonality, meaning we can extract the component of $v$ in $U$ giving us the projection.

Exercise: Find a simple formula for $a_j$ in terms of $v$ and $u_j$

Solution

a_j = \langle v, u_j\rangle

Since orthogonality kills off every other term in

v = a_1u_1 + \dots + a_nu_n + b_1v_1 + \dots + b_nv_n

The above exercise allows us to define the projection $P_U(v)$ of $v$ as

P_U(v) = \langle u_1, v\rangle u_1 + \dots + \langle u_n, v\rangle u_n

Exercise (optional): Prove $P_U : V \to U$ is a linear map (if you know what that means)

Solution

Via substituion and linearity of $\langle\cdot\rangle$ we see

\begin{aligned} P_U(v+w) &= \langle u_1, v+w\rangle u_1 + \dots + \langle u_n, v+w\rangle u_n \\ &= \langle u_1, v\rangle u_1 + \dots + \langle u_n, v\rangle u_n \\ &+ \langle u_1, w\rangle u_1 + \dots + \langle u_n, w\rangle u_n \end{aligned}

The $P_U(\lambda v)$ case is the same.

Furthermore since $P_U(u_j) = u_j$ and $P_U(v_j) = 0$ the matrix of $P_U$ in the $u_1,\dots,v_m$ basis is the identity (for the $u's$ ) followed by zeros (for the $v$ 's)

Notice $P_U(v) = a_1u_1+\dots+a_nu_n$ , we extracted $U$ component of $v$ using inner products and orthogonality!

Now, intuitively it makes sense for $P_U(v)$ to be the closest vector to $v$ , and in $\mathbf R^n$ the intuition is correct. But for arbitrary vector spaces we need a more general argument.

Consider the remainder (error) vector $r = P_U(v) - v$ , the key fact: the remainder is orthogonal to $U$

Exercise: Show $\langle r, u\rangle = 0$ for all $u \in U$ (hint: use $U$ 's basis and linearity of $\langle\cdot\rangle$ )

Solution

Let $u \in U$ and let $c_1,\dots,c_n$ be such that

u = c_1u_1+\dots+c_nu_n

Meaning

\langle r, u\rangle = c_1\langle r, u_1\rangle + \dots + c_n\langle r, u_n\rangle

Now we expand the $r = P_U(v) - v$ part of $\langle r, u_j\rangle$

\begin{aligned} \langle r, u_j\rangle = \langle P_U(v), u_j\rangle - \langle v, u_j\rangle \end{aligned}

Now from the definition of $P_U(v)$ and orthogonality we see $\langle P_U(v), u_j\rangle = \langle v_j, u_j\rangle$ meaning

\langle r, u_j\rangle = \langle P_U(v), u_j\rangle - \langle v, u_j\rangle = 0

Applying this for $j=1,\dots,n$ gives $\langle r, u\rangle = 0$ as desired.

Because of this, any tweak $du \in U$ to $P_U(v)$ can only move us away from $v$ ! We can prove this using the generalized pythagorean theorem since $r$ and $du$ are orthogonal.

\begin{aligned} \|(P_U(v) + du) - v\|^2 &= \|r + du\|^2 \\ &= \|r\|^2 + \|du\|^2 \end{aligned}

This has a minimum at $du = 0$ , meaning we can't do better!

Polynomial approximation

We've covered all the linear algebra we need! It's time to walk through approximating $\sin(x)$ over $[-\pi, \pi]$ with a fifth degree polynomial.

Here's a simplified version of the code, which you should be able to understand!

import sympy as sp
x = sp.Symbol('x')

# function we're approximating
def f(x):
  return sp.sin(x)

a,b = -sp.pi, sp.pi
def inner(f, g):
  return sp.integrate(f*g, (x, a, b))

def normalize(v):
    return v / sp.sqrt(inner(v, v))

# basis of U (polynomials up to degree 5)
B = [1,x,x**2,x**3,x**4,x**5]

# orthogonalize B
O = [normalize(B[0])]
for i in range(1, len(B)):
    O.append(normalize(
        B[i] - sum(
          inner(B[i], O[j])*O[j] # <v_i, e_j>
          for j in range(0, i)
        )
    ))

# get coefficients
coeffs = [inner(f(x), O[j]) for j in range(len(O))]

# turn the coefficients into a sympy polynomial
poly = sum(O[j]*coeffs[j] for j in range(len(coeffs)))

# print the polynomial as latex!
print(sp.latex(poly))
# print the polynomial in numeric form
print(sp.latex(poly.evalf()))
# => 0.00564312 x^{5} - 0.1552714 x^{3} + 0.9878622 x

Full code (with more features) is here. Have fun playing with it!

If you don't understand, tell me! I'll be happy to explain, I want this to be understandable to everyone.

Notation

We denote vectors in a vector space $V$ by $v,w,u \in V$ , If we're dealing with a subspace $U$ , then $u$ denotes a vector $u \in U$ .

Scalars (real numbers) are denoted by $\lambda$ or $a,b,c$ . often when taking linear combinations we have a list of scalars $a_1,\dots,a_n$ .

We denote the inner product between $v$ and $w$ as $\langle v, w\rangle$ . The specific inner product is clear from context. In other sources the dot product is written $v^Tw$ or $v\cdot w$ , these notations are specific to the dot product and don't extend to general inner products.